8.3 Key Predistribution
To use ciphers and authenticators, the communicating participants need to know what keys to use. In the case of a secret-key cipher, how does a pair of participants obtain the key they share? In the case of a public-key cipher, how do participants know what public key belongs to a certain participant? The answer differs depending on whether the keys are short-lived session keys or longer-lived predistributed keys.
A session key is a key used to secure a single, relatively short episode of communication: a session. Each distinct session between a pair of participants uses a new session key, which is always a secret key for speed. The participants determine what session key to use by means of a protocol—a session key establishment protocol. A session key establishment protocol needs its own security (so that, for example, an adversary cannot learn the new session key); that security is based on the longer-lived predistributed keys.
There are two primary motivations for this division of labor between session keys and predistributed keys:
Limiting the amount of time a key is used results in less time for computationally intensive attacks, less ciphertext for cryptanalysis, and less information exposed should the key be broken.
Public key ciphers are generally superior for authentication and session key establishment but too slow to use for encrypting entire messages for confidentiality.
This section explains how predistributed keys are distributed, and the next section will explain how session keys are then established. We henceforth use “Alice” and “Bob” to designate participants, as is common in the cryptography literature. Bear in mind that although we tend to refer to participants in anthropomorphic terms, we are more frequently concerned with the communication between software or hardware entities such as clients and servers that often have no direct relationship with any particular person.
8.3.1 Predistribution of Public Keys
The algorithms to generate a matched pair of public and private keys are publicly known, and software that does it is widely available. So, if Alice wanted to use a public-key cipher, she could generate her own pair of public and private keys, keep the private key hidden, and publicize the public key. But, how can she publicize her public key—assert that it belongs to her—in such a way that other participants can be sure it really belongs to her? Not via email or Web, because an adversary could forge an equally plausible claim that key x belongs to Alice when x really belongs to the adversary.
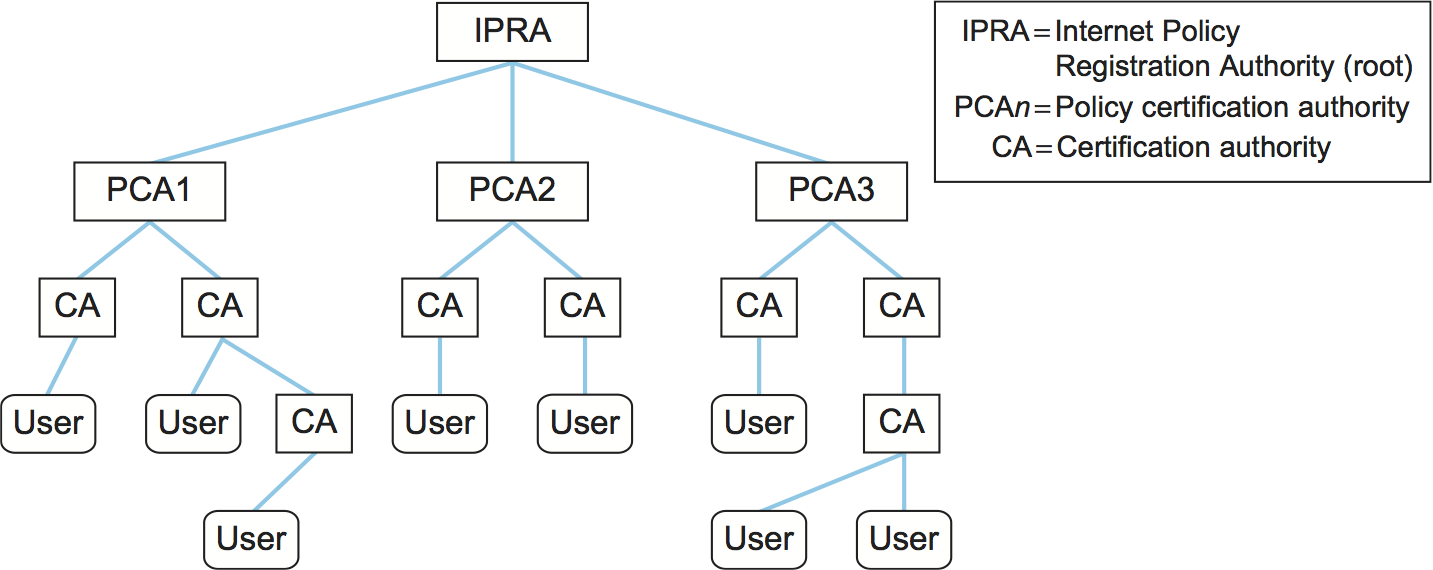
A complete scheme for certifying bindings between public keys and identities—what key belongs to whom—is called a Public Key Infrastructure (PKI). A PKI starts with the ability to verify identities and bind them to keys out of band. By “out of band,” we mean something outside the network and the computers that comprise it, such as in the following If Alice and Bob are individuals who know each other, then they could get together in the same room and Alice could give her public key to Bob directly, perhaps on a business card. If Bob is an organization, Alice the individual could present conventional identification, perhaps involving a photograph or fingerprints. If Alice and Bob are computers owned by the same company, then a system administrator could configure Bob with Alice’s public key.
Establishing keys out of band doesn’t sound like it would scale well, but it suffices to bootstrap a PKI. Bob’s knowledge that Alice’s key is x can be widely, scalably disseminated using a combination of digital signatures and a concept of trust. For example, suppose that you have received Bob’s public key out of band and that you know enough about Bob to trust him on matters of keys and identities. Then Bob could send you a message asserting that Alice’s key is x and—since you already know Bob’s public key—you could authenticate the message as having come from Bob. (Remember that to digitally sign the statement Bob would append a cryptographic hash of it that has been encrypted using his private key.) Since you trust Bob to tell the truth, you would now know that Alice’s key is x, even though you had never met her or exchanged a single message with her. Using digital signatures, Bob wouldn’t even have to send you a message; he could simply create and publish a digitally signed statement that Alice’s key is x. Such a digitally signed statement of a public key binding is called a public key certificate, or simply a certificate. Bob could send Alice a copy of the certificate, or post it on a website. If and when someone needs to verify Alice’s public key, they could do so by getting a copy of the certificate, perhaps directly from Alice—as long as they trust Bob and know his public key. You can see how starting from a very small number of keys (in this case, just Bob’s) you could build up a large set of trusted keys over time. Bob in this case is playing the role often referred to as a certification authority (CA), and much of today’s Internet security depends on CAs. VeriSign is one well-known commercial CA. We return to this topic below.
One of the major standards for certificates is known as X.509. This standard leaves a lot of details open, but specifies a basic structure. A certificate clearly must include:
The identity of the entity being certified
The public key of the entity being certified
The identity of the signer
The digital signature
A digital signature algorithm identifier (which cryptographic hash and which cipher)
An optional component is an expiration time for the certificate. We will see a particular use of this feature below.
Since a certificate creates a binding between an identity and a public key, we should look more closely at what we mean by “identity.” For example, a certificate that says, “This public key belongs to John Smith,” may not be terribly useful if you can’t tell which of the thousands of John Smiths is being identified. Thus, certificates must use a well-defined name space for the identities being certified; for example, certificates are often issued for email addresses and DNS domains.
There are different ways a PKI could formalize the notion of trust. We discuss the two main approaches.
Web of Trust
An alternative model of trust is the web of trust exemplified by Pretty Good Privacy (PGP), which is further discussed in a later section. PGP is a security system for email, so email addresses are the identities to which keys are bound and by which certificates are signed. In keeping with PGP’s roots as protection against government intrusion, there are no CAs. Instead, every individual decides whom they trust and how much they trust them—in this model, trust is a matter of degree. In addition, a public key certificate can include a confidence level indicating how confident the signer is of the key binding claimed in the certificate, so a given user may have to have several certificates attesting to the same key binding before he is willing to trust it.
For example, suppose you have a certificate for Bob provided by Alice; you can assign a moderate level of trust to that certificate. However, if you have additional certificates for Bob that were provided by C and D, each of whom is also moderately trustworthy, that might considerably increase your level of confidence that the public key you have for Bob is valid. In short, PGP recognizes that the problem of establishing trust is quite a personal matter and gives users the raw material to make their own decisions, rather than assuming that they are all willing to trust in a single hierarchical structure of CAs. To quote Phil Zimmerman, the developer of PGP, “PGP is for people who prefer to pack their own parachutes.”
PGP has become quite popular in the networking community, and PGP key-signing parties are a regular feature of various networking events, such as IETF meetings. At these gatherings, an individual can
Collect public keys from others whose identity he knows.
Provide his public key to others.
Get his public key signed by others, thus collecting certificates that will be persuasive to an increasingly large set of people.
Sign the public key of other individuals, thus helping them build up their set of certificates that they can use to distribute their public keys.
Collect certificates from other individuals whom he trusts enough to sign keys.
Thus, over time, a user will collect a set of certificates with varying degrees of trust.
Certificate Revocation
One issue that arises with certificates is how to revoke, or undo, a certificate. Why is this important? Suppose that you suspect that someone has discovered your private key. There may be any number of certificates in the universe that assert that you are the owner of the public key corresponding to that private key. The person who discovered your private key thus has everything he needs to impersonate you: valid certificates and your private key. To solve this problem, it would be nice to be able to revoke the certificates that bind your old, compromised key to your identity, so that the impersonator will no longer be able to persuade other people that he is you.
The basic solution to the problem is simple enough. Each CA can issue a certificate revocation list (CRL), which is a digitally signed list of certificates that have been revoked. The CRL is periodically updated and made publicly available. Because it is digitally signed, it can just be posted on a website. Now, when Alice receives a certificate for Bob that she wants to verify, she will first consult the latest CRL issued by the CA. As long as the certificate has not been revoked, it is valid. Note that, if all certificates have unlimited life spans, the CRL would always be getting longer, since you could never take a certificate off the CRL for fear that some copy of the revoked certificate might be used. For this reason, it is common to attach an expiration date to a certificate when it is issued. Thus, we can limit the length of time that a revoked certificate needs to stay on a CRL. As soon as its original expiration date is passed, it can be removed from the CRL.
8.3.2 Predistribution of Secret Keys
If Alice wants to use a secret-key cipher to communicate with Bob, she can’t just pick a key and send it to him because, without already having a key, they can’t encrypt this key to keep it confidential and they can’t authenticate each other. As with public keys, some predistribution scheme is needed. Predistribution is harder for secret keys than for public keys for two obvious reasons:
While only one public key per entity is sufficient for authentication and confidentiality, there must be a secret key for each pair of entities who wish to communicate. If there are N entities, that means N(N-1)/2 keys.
Unlike public keys, secret keys must be kept secret.
In summary, there are a lot more keys to distribute, and you can’t use certificates that everyone can read.
The most common solution is to use a Key Distribution Center (KDC). A KDC is a trusted entity that shares a secret key with each other entity. This brings the number of keys down to a more manageable N-1, few enough to establish out of band for some applications. When Alice wishes to communicate with Bob, that communication does not travel via the KDC. Rather, the KDC participates in a protocol that authenticates Alice and Bob—using the keys that the KDC already shares with each of them—and generates a new session key for them to use. Then Alice and Bob communicate directly using their session key. Kerberos is a widely used system based on this approach. We describe Kerberos (which also provides authentication) in the next section. The following subsection describes a powerful alternative.
8.3.3 Diffie-Hellman Key Exchange
Another approach to establishing a shared secret key is to use the Diffie-Hellman key exchange protocol, which works without using any predistributed keys. The messages exchanged between Alice and Bob can be read by anyone able to eavesdrop, and yet the eavesdropper won’t know the secret key that Alice and Bob end up with.
Diffie-Hellman doesn’t authenticate the participants. Since it is rarely useful to communicate securely without being sure whom you’re communicating with, Diffie-Hellman is usually augmented in some way to provide authentication. One of the main uses of Diffie-Hellman is in the Internet Key Exchange (IKE) protocol, a central part of the IP Security (IPsec) architecture.
The Diffie-Hellman protocol has two parameters, p and g, both of which are public and may be used by all the users in a particular system. Parameter p must be a prime number. The integers \(\bmod p\) (short for modulo p) are \(0\) through p-1, since \(x \bmod p\) is the remainder after x is divided by p, and form what mathematicians call a group under multiplication. Parameter g (usually called a generator) must be a primitive root of p: For every number n from 1 through p-1 there must be some value k such that \(n = g^k \bmod p\). For example, if p were the prime number 5 (a real system would use a much larger number), then we might choose 2 to be the generator g since:
Suppose Alice and Bob want to agree on a shared secret key. Alice and Bob, and everyone else, already know the values of p and g. Alice generates a random private value a and Bob generates a random private value b. Both a and b are drawn from the set of integers \(\{1,\dots{}, p-1\}\). Alice and Bob derive their corresponding public values—the values they will send to each other unencrypted—as follows. Alice’s public value is
and Bob’s public value is
They then exchange their public values. Finally, Alice computes
and Bob computes
Alice and Bob now have \(g^{ab} \bmod p\) (which is equal to \(g^{ba} \bmod p)\) as their shared secret key.
Any eavesdropper would know p, g, and the two public values \(g^a \bmod p\) and \(g^b \bmod p\). If only the eavesdropper could determine a or b, she could easily compute the resulting key. Determining a or b from that information is, however, computationally infeasible for suitably large p,a, and b; it is known as the discrete logarithm problem.
For example, using p = 5 and g = 2 from above, suppose Alice picks the random number a = 3 and Bob picks the random number b = 4. Then Alice sends Bob the public value
and Bob sends Alice the public value
Alice is then able to compute
by substituting Bob’s public value for \((2^b \bmod 5)\). Similarly, Bob is able to compute
by substituting Alice’s public value for \((2^a \bmod 5)\). Both Alice and Bob now agree that the secret key is \(1\).
There is the problem of Diffie-Hellman’s lack of authentication. One attack that can take advantage of this is the man-in-the-middle attack. Suppose Mallory is an adversary with the ability to intercept messages. Mallory already knows p and g since they are public, and she generates random private values \(c\) and \(d\) to use with Alice and Bob, respectively. When Alice and Bob send their public values to each other, Mallory intercepts them and sends her own public values, as in Figure 201. The result is that Alice and Bob each end up unknowingly sharing a key with Mallory instead of each other.
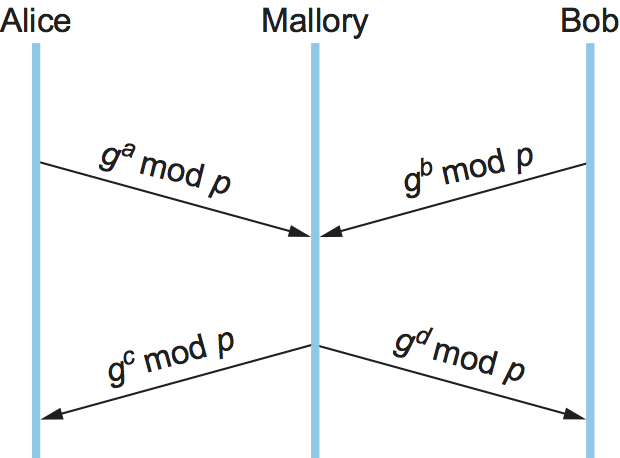
Figure 201. A man-in-the-middle attack.
A variant of Diffie-Hellman sometimes called fixed Diffie-Hellman supports authentication of one or both participants. It relies on certificates that are similar to public key certificates but instead certify the Diffie-Hellman public parameters of an entity. For example, such a certificate would state that Alice’s Diffie-Hellman parameters are p, g, and \(g^a \bmod p\) (note that the value of a would still be known only to Alice). Such a certificate would assure Bob that the other participant in Diffie-Hellman is Alice—or else the other participant won’t be able to compute the secret key, because she won’t know a. If both participants have certificates for their Diffie-Hellman parameters, they can authenticate each other. If just one has a certificate, then just that one can be authenticated. This is useful in some situations; for example, when one participant is a web server and the other is an arbitrary client, the client can authenticate the web server and establish a secret key for confidentiality before sending a credit card number to the web server.